[Quantum Chemistry] 파동 (Wave)

# Introduction

 

이번 포스팅에서는 양자화학에 대한 내용을 다뤄볼 예정입니다. 기본적으로 내용은 I.N. Levine, "Quantum Chemistry" 7th Ed. Prentice Hall (2014)을 바탕으로 알아볼 것입니다. 개인적으로 양자화학을 공부하기에 좋은 책이라 생각됩니다. 이전에 물리 화학(Physical Chemistry)에서도 양자화학을 다뤘는데 ^[각주:1] 궁금하신 분 들은 참고하셔도 좋을 것 같습니다.

 

# Wave

 

파동(Wave)는 매질을 통해 운동이나 에너지가 전달되는 현상입니다. 에너지 자체는 시간이 지남에 따라서 공간상으로 퍼져나가지만 매질 자체는 운동을 매개할 뿐 이동하지 않습니다. 특히, 전자기파는 매질 없이 전달되는 파동이며 양자역학에서도 파동은 매질 없이 정의되는 근본적인 개념이며, 물질의 기본 성질로 파동성^[각주:2]을 이야기합니다.

 

Fig 1. Surface Wave

세면대의 수도꼭지에서 물방울이 떨어진다면 Fig 1^[각주:3]과 같이 물방울에 의해 파동이 생기게 될 것입니다. 이때, 평면파(2차원)를 1차원적으로 바라본다면 Fig 2와 같은 파동을 확인할 수 있을 것입니다.

Fig 2. Wave

이러한 파동을 가장 잘 표현할 수 있는 수학적인 형태는 쉽게 짐작할 수 있듯이 sin 함수와 cos 함수입니다. 흔히 파동을 다룰 때 다음과 같은 식을 활용합니다. 이때, A는 진폭(Amplitude), k는 파수(wave number),  ω는 진동수(frequency)를 의미합니다.

 

Equation (1)

x축에 놓여있는 용수철을 잡고 y축 방향으로 흔드는 상황을 상상해봅시다. Equation (1)에서 A는 용수철을 얼마나 크게 흔들 것인가를 의미할 것이며, ω는 용수철을 얼마나 빠르게 흔들 것 인가를 의미할 것입니다. Equation (1)에서 파동의 운동 에너지를 구하기 위해 y를 t에 대해 미분을 진행하면 y축에 대한 속도를 얻을 수 있고, 이를 바탕으로 운동에너지를 구하면,

 

Equation (2)

Equation (3)

Equation (3)를 바탕으로 파동의 운동에너지를 결정하는 중요한 요소는 "얼마나 크게(A)"와 "얼마나 빠르게(ω)"임을 알 수 있습니다. 파동은 입자가 움직이는 것과 다르게 질량 요소가 위-아래(y축)로만 움직이지만, x축을 따라서 움직이는 것처럼 보입니다. 이를 수식적으로 표현해봅시다. 

 

Equation (4)

Equation (5)

파동이 한번 진동하기 위한 시간은 Equation (4)와 같을 것이며, 파동의 파장은 Equation (5)와 같을 것입니다. 즉, 파동의 속도는 Equation (6)으로 표현됩니다.

Equation (6)

Equation (6)을 바탕으로 파동의 운동에너지를 표현하면, Equation (7)과 같습니다.

 

Equation (7)

#Wave Equation

 

파동 방정식을 구하기 위해서 Equation (1)을 x와 t에 대해서 2번 미분하면, 

 

Equation (8)

Equation (9)

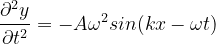
Equation (8)과 Equation (9)에서 공통되는 항이 존재함을 알 수 있습니다. Equation (6)을 ω에 대해 정리^[각주:4]해서 Equation(9)에 대입하고, Equation(8)로 치환하면 다음과 같은 파동 방정식을 얻을 수 있습니다.

 

Equation (10)

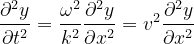
Equation (10)을 3차원으로 확장하면 Equation (11)과 같습니다.

 

Equation (11)

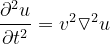
파동방정식을 만족하는 해는 Equation (1) 뿐만 아니라 다음과 같은 다양한 형태가 존재하는데,

 

이러한 해들의 일반적인 형태는 오일러 공식 ^[각주:5]을 통해 Equation (12)와 같이 표현할 수 있습니다. Equation (12)를 파동 방정식에 대입해도 성립하는 것을 확인할 수 있습니다. 

 

Equation (12)

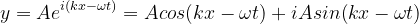
Equation (12)로 표현되는 파동들을 중첩시키면 더 일반적인 해에 해당하는 Equation (13)을 얻을 수 있습니다.

 

Equation (13)

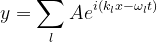
특히, 양자역학을 공부하면 오일러 공식으로 표현되는 파동 Equation (12)를 자주 접하게 됩니다. Equation (12)와 같은 형태는 복소수(Complex number)로 다음 포스팅에 자세하게 알아볼 것입니다.

---

 

1. d2illy.tistory.com/23?category=867342 [본문으로]
2. d2illy.tistory.com/25?category=867342 [본문으로]
3. 출처 : en.wikipedia.org/wiki/Wave [본문으로]
4. ω=kv [본문으로]
5. en.wikipedia.org/wiki/Euler%27s_formula [본문으로]