| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
- Physical Chemistry
- 타이베이
- Aromaticity
- 화학
- 양자화학
- Gaussian
- 대만
- 물리화학
- quantum chemistry
- Chemistry
- 유기화학
- travel
- 양자역학
- Organic Chemistry
- 여행
- Computational Chemistry
- Today
- Total
Daily Project
[Quantum Chemistry] 복소수 (Complex number) 본문
[Quantum Chemistry] 복소수 (Complex number)
Jun_Hyeong 2021. 5. 11. 00:18
#KeyWords
복소수(Complex number), 복소 평면(Complex plane),
켤례 복소수(Complex conjugate), 오일러 공식(Euler's formula)
# Introduction
이전 포스팅에서 언급했던 복소수(Complex number)에 대해서 알아보고 관련된 성질들을 알아볼 것입니다.
# Complex number
복소수 z는 다음과 같은 꼴을 가지고 있습니다.

이때, x와 y는 실수(real number)로 x는 복소수 z의 실수 부분(real part)라고 부르며 y는 허수 부분(imaginary part)라고 부릅니다. Equation(1)에서 y=0이면 z는 실수(real number)에 해당하며, y≠0이면 z가 허수(imaginary number)가 됩니다.
복소수 z는 복소평면(Complex plane), x축은 실수 부분에 해당하고 y축은 허수 부분에 해당하는 평면에 나타낼 수 있습니다. 예를 들어 z=2+i를 복소평면에 표현한다면 Figure (1)과 같이 표현할 수 있다는 것입니다.

Figure (1)에서 직관적으로 생각할 수 있는 요소가 2가지 있습니다. 첫 번째는 절댓값(absolute value)으로 |z|로 표현되며, 복소수 z와 원점 사이의 거리에 해당합니다. 두 번째는 위상(phase)으로 θ로 표현되며, 원점과 복소수 z를 이은 벡터와 양의 x축이 이루는 각도를 뜻합니다. 즉, 복소수 z는 다음과 같이 표현할 수 있습니다.


Equation (2)를 오일러 공식, Equation (3)를 이용해 정리하면 Equation (4)로 표현할 수 있습니다.


여기서, 켤례 복소수(Complex conjugate)를 정의해볼 것입니다. z를 x + iy라고 정의하면 간단하게 z의 켤례 복소수는 x - iy를 뜻합니다. 즉,

만약 복소수 z의 허수 부분이 0이라면 z=z*이 성립1하고, 모든 복소수에 대해서 (z*)*=z 2가 성립합니다. 복소수 z와 켤례 복소수 z*를 복소 평면에 나타내면 Figure (2)3 를 얻을 수 있습니다.

더 나아가, 복소수 z와 z의 켤례 복소수를 곱하면, 즉 Equation (1)과 Equation (5)를 곱하면,

복소수 z의 절댓값의 제곱을 얻을 수 있습니다. 더 나아가서 서로 크기와 위상이 다른 복소수 2개에 대해서,

서로를 곱하면 Equation (8), 나누면 Equation (9)가 성립함을 지수법칙을 통해서 쉽게 알 수 있습니다.


또한, 2개의 복소수의 켤례 복소수의 경우 다음과 같이 계산할 수 있습니다.




양자화학을 공부할 때 복소수 자체를 자주 쓰기도 하지만, 복소수로 구성된 행렬도 자주 사용됩니다. 복소 행렬의 경우 켤례 전치(Conjugate transpose)4가 등장하는데, 켤례 복소수와 마찬가지로 A*5을 사용합니다.

하지만, 복소 행렬의 경우 Equation (10)이 성립하지 않고 Equation (12)가 성립하는 것을 알아두어야 합니다. 즉, 다루는 대상이 무엇인지를 판별하고 conjugate를 하는 것이 중요하다는 것입니다. 이 작업의 중요성은 뒤에 Hermitain operator가 등장하고 연산을 할 때 다시 알아볼 것 입니다.

결국 양자화학에서 관심이 있는 것은 system을 표현하는 파동 함수(wave function, ψ)입니다. 파동 함수에서 정보를 얻어오기 위해서 파동 함수끼리의 연산이 필수적이고, 파동 함수는 흔히 복소수의 형태를 가지고 있으므로 복소수와 이들의 연산에 대해 아는 것은 매우 중요합니다.
#Problem
1. 다음의 복소수의 absolute value와 phase를 구하시오

Ans)
(a) 4, π (b) 2, 3/2π (c) 3√5, 0.4636π (tan^(-1)0.5) (d) 2, π/5
2. 다음의 복소수의 complex conjugate를 구하시오

Ans)
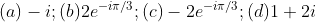
3. 다음이 성립함을 증명하시오.

Ans)
Equation (3)를 Problem (3)에 대입하면 성립함을 알 수 있다.
- x+0i=(x+0i)* [본문으로]
- (x-iy)*=x+iy [본문으로]
- 출처 : ko.wikipedia.org/wiki/%EB%B3%B5%EC%86%8C%EC%88%98 [본문으로]
- en.wikipedia.org/wiki/Conjugate_transpose [본문으로]
- A* 대신 A†를 사용하기도 함 [본문으로]
'Chemistry Project > Quantum Chemistry' 카테고리의 다른 글
| [Quantum Chemistry] 디락 표기법(Dirac Notation) (0) | 2021.06.27 |
|---|---|
| [Quantum Chemistry] 연산자 (Operator) - 1 (0) | 2021.06.27 |
| [Quantum Chemistry] 양자역학적 에너지(QM Energy) (0) | 2021.05.19 |
| [Quantum Chemistry] 파동 (Wave) (0) | 2021.04.29 |




