| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 화학
- 타이베이
- travel
- quantum chemistry
- 대만
- 양자화학
- Aromaticity
- 양자역학
- Chemistry
- Physical Chemistry
- Gaussian
- 여행
- Organic Chemistry
- 물리화학
- 유기화학
- Computational Chemistry
- Today
- Total
Daily Project
[Quantum Chemistry] 양자역학적 에너지(QM Energy) 본문
[Quantum Chemistry] 양자역학적 에너지(QM Energy)
Jun_Hyeong 2021. 5. 19. 00:28
#Introduction
양자역학이 발전함에 따라 현대 원자 모형이 등장하게 되었습니다. 이를 바탕으로 양자역학의 기초에 대해 알아볼 것입니다.
#Classical mechanical description of atom
역사적으로 원자 구조를 설명하기 위한 시도가 많았습니다. 돌턴 모형과 톰슨 모형, 러더퍼드 모형, 보어 모형 등 시간이 지남에 따라서 실험적으로 밝혀진 사실을 설명하기 위해 원자 모형 또한 변해왔습니다. 그중에서 러더퍼드 모형을 먼저 살펴봅시다..
러더퍼드 원자 모형의 경우 질량의 대부분이 뭉쳐있는 핵이 존재하며 그 주위를 전자가 돌고 있다고 설명합니다. 그러나 고전 전자기학의 라모 공식에 따르면 가속하는 전자는 전자기파를 방출하는데, 이에 따라 궤도를 도는 전자의 에너지는 점차 에너지를 잃고 핵에 충돌하게 됩니다.
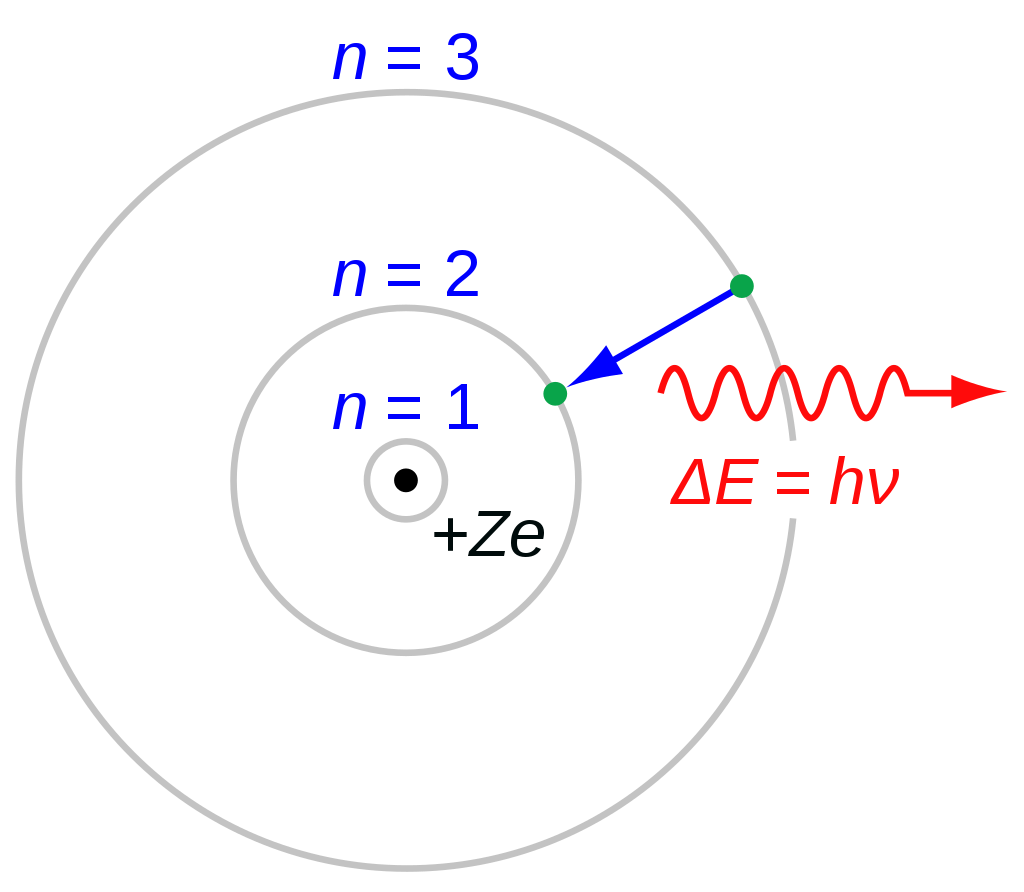
이러한 문제를 해결하기 위해 보어는 전자가 오직 정해진 각운동량과 에너지를 가지는 특정한 준위의 궤도에서만 돌 수 있다는 아이디어를 이용해 보어 원자 모형을 제안합니다. 그러나 보어 모형은 오직 수소의 스펙트럼 선만을 예측할 수 있으며 다전자 원자의 경우 설명할 수 없었습니다. 더 나아가 분광학이 발전함에 따라서 설명할 수 없는 수소 스펙트럼 선이 발견되기도 하였습니다.
#Quantum mechanical description of atom
루이 드브로이가 모든 움직이는 입자는 파동과 같은 성질을 가진다는 것을 제시함에 따라서, 움직이는 전자의 성질을 파동으로 설명해보려는 시도가 생기게 됩니다. 그 결과 전자 궤도가 존재하지 않고 전자를 발견할 확률 만을 알 수 있다는 현대 원자 모형이 성립됩니다.
전하 +e를 가지는 원자 핵과 전하 -e를 가지는 전자 사이의 potential energy는 Equation (1)과 같습니다. 그렇다면 전자의 거동을 표현하는 함수를 파동 함수 ψ라고 가정하고, 확률 밀도 함수를 |ψ|2라고 정의해봅시다. 이를 이용해서 전자의 potential energy를 표현해보면,


Equation (2)로 표현할 수 있습니다. 이는 전자가 존재할 수 있는 x, y, z 좌표에서 Equation (1)에 전자의 존재 확률을 곱해준 것과 같습니다. 만약, |ψ|2가 구면 좌표계로 표현할 수 있다면,

Equation (3)와 같이 나타낼 수 있고,
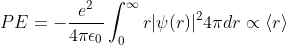
이때, <r>은 전자와 핵의 거리의 평균값1을 의미합니다. 자세한 내용은 다른 포스팅에서 다루겠습니다. 즉, Potential Energy는 전자와 핵의 거리가 가까워질수록 작아집니다. 즉, 전자가 핵에 충돌한다는 결말로 이어집니다.
이러한 문제점을 해결하기 위해서 운동 에너지(kinetic energy)를 도입해야 합니다. 이전 포스팅2에서 파동의 운동에너지는 k2과 관련 있다는 사실을 확인했습니다. Equation (4)와 같이 u를 일반적인 파동 방정식으로 표현하고 x에 대해서 편미분을 두 번 진행하면 k2를 얻을 수 있습니다.

즉, 운동 에너지는

과 관련된 무엇이라는 추측을 할 수 있습니다. 그렇다면 양자역학적 Kinetic energy를 정의해봅시다. 드브로이의 물질파 이론에 따라 Equation (7)가 성립합니다.

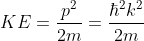
Equation (5)에서 얻었던 영감을 바탕으로 Equation (6)과 같이 Kinetic energy를 정의할 수 있습니다. 3
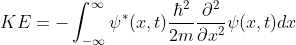
Equation (8)에 Equation (5)의 u를 대입하면 Eqaution (7)을 얻을 수 있습니다. Equation (8)을 부분 적분을 이용해서 전개하면,


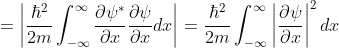
Equation (9)를 얻을 수 있고, 이를 바탕으로 양자역학적 Kinetic energy는 파동 함수의 기울기의 제곱에 비례한다는 사실을 알 수 있습니다. Potential energy와는 다르게 <r>이 커지면 Kinetic energy는 더 작아지게 됩니다. 이를 그림으로 표현하면 Figure 3와 같습니다4.

파동함수 ψ의 <r>이 작아지면 ψ의 slope가 증가하게 되고 반대로 <r>이 커지면 ψ의 slope가 작아집니다. 즉, Kinetic energy와 Potential energy는 경쟁하는 관계라는 사실을 알 수 있습니다. 그러므로 KE와 PE가 균형을 이룸으로써 원자가 크기를 가질 수 있는 것입니다. 이를 원자의 에너지적 측면에서 보면 Figure 4로 표현할 수 있는데, KE와 PE가 균형을 이루는 지점이 제일 작은 에너지 값을 가지는 <r>입니다. 수소 원자의 경우 이 지점의 r을 보어 반지름(a0)로 표현합니다.

- |ψ|2가 확률 밀도 함수이므로 r의 평균 값 [본문으로]
- https://d2illy.tistory.com/54 [본문으로]
- 이때, Potential energy를 표현한 Equation (2)와 동일한 구조로 이루어져 있다는 것이 중요합니다. 실제로 ψ는 복소함수이기 때문에 Equation (8)과 같은 꼴로 표현해야 합니다. [본문으로]
- 파동함수 ψ에서 핵과 전자의 평균 거리, <r>과 ψ의 slope [본문으로]
'Chemistry Project > Quantum Chemistry' 카테고리의 다른 글
| [Quantum Chemistry] 디락 표기법(Dirac Notation) (0) | 2021.06.27 |
|---|---|
| [Quantum Chemistry] 연산자 (Operator) - 1 (0) | 2021.06.27 |
| [Quantum Chemistry] 복소수 (Complex number) (0) | 2021.05.11 |
| [Quantum Chemistry] 파동 (Wave) (0) | 2021.04.29 |




