| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 여행
- Gaussian
- 유기화학
- travel
- 양자화학
- Computational Chemistry
- 화학
- Chemistry
- 타이베이
- Aromaticity
- quantum chemistry
- Organic Chemistry
- 물리화학
- 대만
- Physical Chemistry
- 양자역학
- Today
- Total
Daily Project
[Quantum Chemistry] 디락 표기법(Dirac Notation) 본문
[Quantum Chemistry] 디락 표기법(Dirac Notation)
Jun_Hyeong 2021. 6. 27. 22:03
#Introduction
모든 분야에서 있는 사실 그대로를 표현한다면 시간이 많이 들고 복잡해서 알아보기 힘들어집니다. 이럴 때 간결하고 알아보기 쉽게 만들어주는 표기법을 사용합니다. 비슷하게, 양자역학에서 모든 식을 그대로 적는 것은 매우 비효율적입니다. 이를 위해서 양자 상태를 표현하는 표준 표기법인 디락 표기법(Dirac Notation)을 알아보겠습니다.
# Why Dirac Notation?
이전 포스팅 1에서 Kinetic Energy는 다음과 같이 나타나는 것을 알아보았습니다.
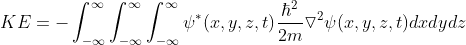
이러한 식을 하나만 적는다면 Equation (1)을 그대로 적어도 상관없겠지만, 다루는 시스템이 커지면 커질수록 모든 항을 그대로 적는 것보다 간결하게 표기할 수 있는 방법이 필요해집니다. 이때, 양자역학에서 양자 상태를 표현하는 표준 표기법인 Dirac notation을 사용합니다. 먼저, Equation (1)을 Dirac Notation을 이용해 표현하면,

Equation (1)과 Equation (2)를 비교하면 확실하게 Dirac Notation을 사용하는 것이 간결하다는 것을 알 수 있습니다.
# What is Dirac Notation?
Dirac Notation은 "⟨" 와 "⟩", "|"을 이용해서 표현하는데, ⟨ψ|에 해당하는 부분을 Bra라고 부르고 |ψ⟩에 해당하는 부분을 Ket이라고 부릅니다.
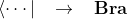

브라와 켓은 각각 행 벡터(Column vector)와 열 벡터(Row vector)에 해당합니다. 특정한 고유 함수 집합 φ가 N차원 힐베르트 공간을 이루고 있다면, 브라는 Equation (5)와 같이 켓은 Equation (6)과 같이 표현합니다. 이때, *는 켤레 복소수입니다.


Equation (5)와 Equation (6)의 관계를 살펴봅시다. Equation (5)에 켤레 전치(conjugate transpose)2 혹은 에르미트 수반(Hermitian adjoint)을 취하면 Equation (6)가 됨을 확인할 수 있습니다. 즉,

이 성립합니다. 행렬 표기법을 브라와 켓을 곱하면 다음 식을 얻을 수 있는데, Equaion (8)은 내적(Equation (9)에 해당합니다.


디락 표기법을 통해 내적을 표현할 수 있으니 연산자의 평균값의 표현도 가능합니다. 즉, Equation (10)과 같이 표현합니다.

디락 표기법에 켤레 전치를 취하는 경우 Equation (11)이 성립합니다.

Eqaution (11)을 바탕으로 Equation (10)을 확장시키면, Equation (12)에 의해서 Eqaution (13)이 성립함을 확인할 수 있습니다.
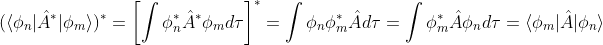

만약, 항에 상수가 있다면 다음과 같이 브라-캣의 바깥으로 꺼낼 수 있습니다.

Equation (10)과 Eqaution (14)를 이용하면 Equation (1)을 Equation (2)로 표현할 수 있음을 알 수 있습니다.
#Problem
1. f 와 g는 함수이고 c는 상수, B는 선형 연산자일 때 식 (a)와 (b), (c)가 성립하는가? T or F
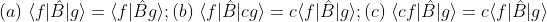
Ans : (a) True; (b) True; (c) False
2. 다음 식이 성립할 조건은?

Ans : c = c*
3. 선형 연산자 B가 B=B*를 만족할 때 다음식이 성립함을 보이시오.

Ans :
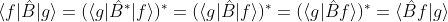
- https://d2illy.tistory.com/56 [본문으로]
- 특정 행렬의 전치 행렬에 성분 별 켤레 복소수를 취하는 것 [본문으로]
'Chemistry Project > Quantum Chemistry' 카테고리의 다른 글
| [Quantum Chemistry] 연산자 (Operator) - 1 (0) | 2021.06.27 |
|---|---|
| [Quantum Chemistry] 양자역학적 에너지(QM Energy) (0) | 2021.05.19 |
| [Quantum Chemistry] 복소수 (Complex number) (0) | 2021.05.11 |
| [Quantum Chemistry] 파동 (Wave) (0) | 2021.04.29 |




